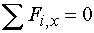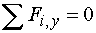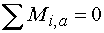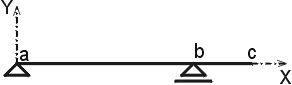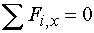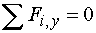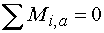Konzola - vektnutý nosník
!!! Stránka ve výstavbě !!!
Konzolou (neboli vetknutým nosníkem) rozumíme přímý nosník, jehož jeden konec
je vetknut a druhý konec je volný.


Vetknutí je typ podepření, které zabraňuje posunu místa podepření ve vodorovném
i svislém směru a také zabraňuje pootočení místa podepření. Ve vetknutí vznikají
od zatížení tři složky reakcí.
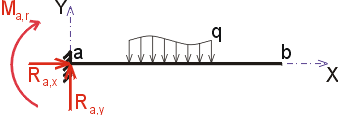
Postup řešení konzoly je obdobný jako u prostého nosníku.
Nejprve určíme reakce z podmínek rovnováhy :
1. Součet všech sil působících ve směru osy x je roven nule
2. Součet všech sil působících ve směru osy y je roven nule
3. Součet momentů k libovolnému bodu od zatížení je roven nule
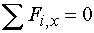
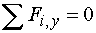
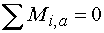
Poté určíme vnitřní síly a vykreslíme obrazce průběhu vnitřních sil. Princip výpočtů
vnitřních sil na konzole ale i na všech ostatních prutových konstrukcích je shodný
jako u prostého nosníku.
Příklad 7.1 |
Prostý nosník s převislými konci
Prostým nosníkem s převislými konci rozumíme přímý nosník, jež je prostě podepřen,
ne však nutně na svých koncích, jako tomu bylo u prostého nosníku.
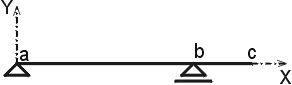


Postup řešení je opět shodný.
Nejprve určíme reakce z podmínek rovnováhy :
1. Součet všech sil působících ve směru osy x je roven nule
2. Součet všech sil působících ve směru osy y je roven nule
3. Součet momentů k libovolnému bodu od zatížení je roven nule
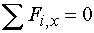
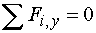
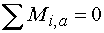
Poté určíme vnitřní síly a vykreslíme obrazce průběhu vnitřních sil.
Příklad 7.2 |