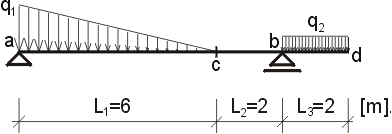
q1 = 9 kN/m, q1 = 3 kN/m,
Prostý nosník s převislými konci - příklad 7.2

|
Určete reakce a průběhy vnitřních sil na zadaném prostém nosníku s převislými konci. q1 = 9 kN/m, q1 = 3 kN/m, |
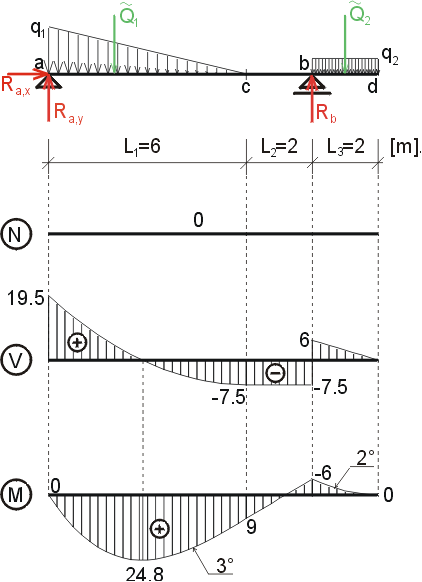
|
1) Výpočet reakcíNejprve nahradíme spojité lineární zatížení q1 a spojité rovnoměrné zatížení q2 náhradními břemenemy :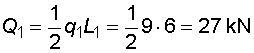 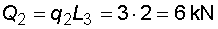 Nosník s převislým koncem je v bodě a podepřen pevným neposuvným kloubem, ve kterém vzniknou dvě složky reakcí Ra,x a Ra,y. V bodě b je nosník podepřen posuvným kloubem, ve kterém vznikne jedna složka reakce Rb. Velikosti složek reakcí dostaneme z podmínek rovnováhy : 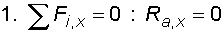 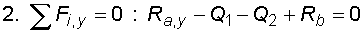 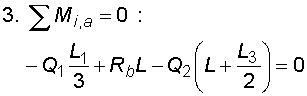 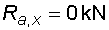 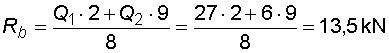 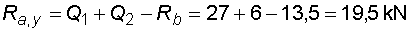 |

|
2) Výpočet vnitřních silNormálové sílyNa celém nosníku nepůsobí ve směru osy x žádné zatížení, a proto normálové síly jsou na celém nosníku nulové :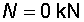 Posouvající sílyPosouvající síly vyvodí složky reakcí Ra,y, Rb a spojitá zatížení q1, q2, jež máme nahrazena náhradními břemeny Q1 a Q2. Hodnoty posouvajících sil v jednotlivých řezech jsou :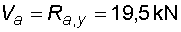 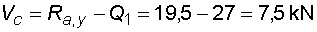 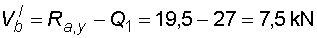 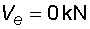 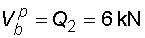 Tvar průběhu posouvajících sil odpovídá zatížení. Mezi body a,c je zatížení lineární, posouvající síla musí být tvaru paraboly 2°. Mezi body b,d je zatížení konstantní, takže průběh posouvajících sil bude lineární. Mezi body c,b není spojité zatížení, a tudíž posouvající síly budou konstantní. Mezi body a,c protíná graf posouvajících sil osu nosníku. V tomto místě vzniká nebezpečný průřez a je třeba toto místo stanovit. Postup byl uveden v příkladu 6.2, takže zde uvádím je použité vztahy : 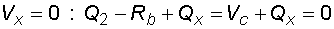 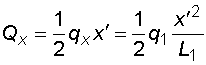 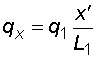 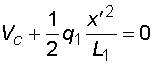 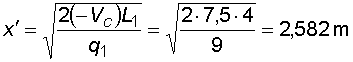 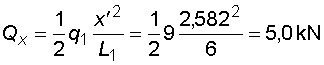 Ohybové momentyOhybové momenty (stejně jako ostatní vnitřní síly) se určují pořád podle stejného principu. Vyvodí je zatížení, jež působí příčně na osu nosníku. Hodnoty v jednotlivých řezech dostaneme ze vztahů :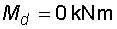 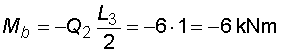 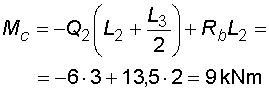 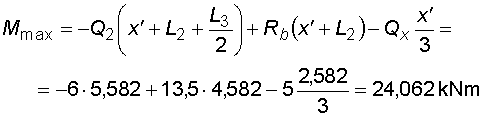 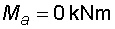 Průběh momentů určíme s pomocí posouvajících sil. Mezi body a,c májí posouvající síly průběh tvaru paraboly 2°, ohybový moment bude mít mezi těmito body tedy tvar paraboly 3°. Mezi body b,d je posouvající síla lineární, proto moment bude mít tvar paraboly 2°. Mezi body c,b je posouvající síla konstantní, tvar momentů tak bude lineární. |