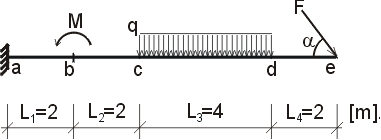
F = 30 kN, cosa = 0.6, sina = 0.8, M = 50 kNm, q = 9 kN/m,
Konzola - příklad 7.1

|
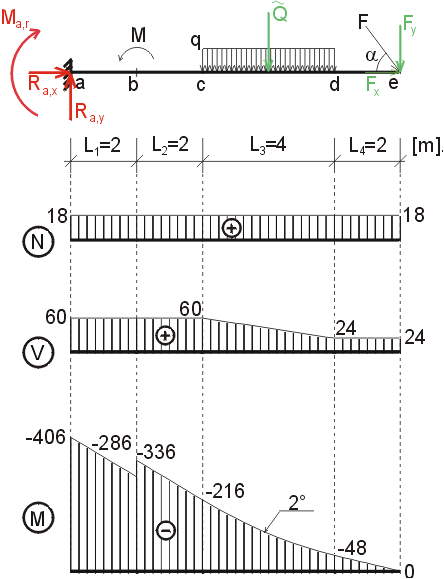
Určete reakce a průběhy vnitřních sil na zadaném konzolovém nosníku. F = 30 kN, cosa = 0.6, sina = 0.8, M = 50 kNm, q = 9 kN/m, |
|
1) Výpočet reakcíNejprve nahradíme spojité rovnoměrné zatížení q náhradním břemenem Q a rozložíme sílu F na složky Fx a Fy :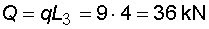 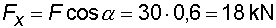 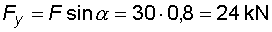 Konzolový nosník je v bodě a vetknut. V tomto místě vzniknou tři složky reakcí : Ra,x, Ra,y a Ma,r. Jejich velikosti získáme z podmínek rovnováhy : 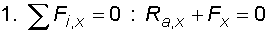 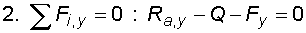 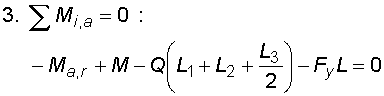 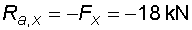 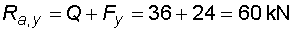 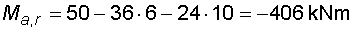 |

|
2) Výpočet vnitřních silNormálové sílyVe směru osy nosníku působí pouze složky Ra,x a Fx na koncích nosníku, proto průběh normálových sil bude po celé délce konstantní a bude mít velikost :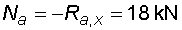 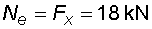 Posouvající sílyPosouvající síly vyvodí zatížení, které působí kolmo na osu nosníku. V našem případě to jsou složky Ra,y, Fy a spojité rovnoměrné zatížení q, jež je nahrazeno náhradním břemenem Q. Ze zatížení je patrné, že průběh posouvajících sil bude mezi body a,c a d,e konstantní a mezi body c,d bude lineární. Hodnoty v jednotlivých řezech dostaneme ze vztahů :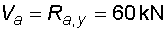 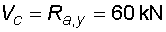 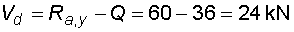 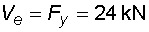 Ohybové momentyOhybové momenty vyvodí v našem případě pouze zatížení ve směru osy y. Hodnoty v jednotlivých řezech dostaneme ze vztahů :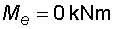 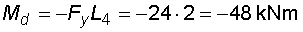 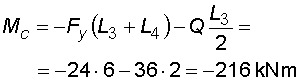 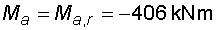 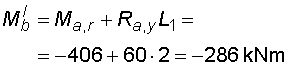 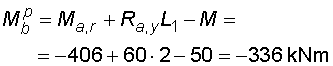 Průběh momentů úzce souvisí s posouvajicími silami a zatížením (viz. diferenciální podmínky rovnováhy). Máme-li vykreleny posouvající síly, můžeme určit průběh momentů. Mezi body a,d a e,b je posouvající síla konstantní, moment bude tedy lineární. V bodě c působí osamělý moment M, proto v tomto místě bude v průběhu nespojitost (skok v grafu). Mezi body d,e je posouvající síla lineární, moment bude mít tedy tvar paraboly 2°. |